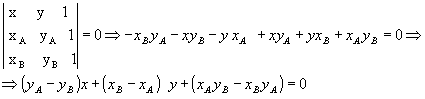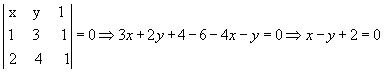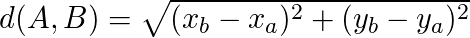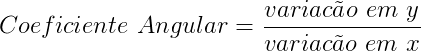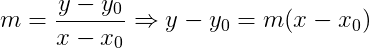MATEMÁTICA - 3º SÉRIE

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 3º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 23/03 à 27/03. (PARTE 2) 


QUERIDOS ALUNOS,
PESQUISA:

• ELABORAR UM MAPA MENTAL MATEMÁTICO SOBRE GEOMETRIA ANALÍTICA.

LEMBRANDO QUE UM MAPA MENTAL, É O MESMO QUE UM RESUMO, PORÉM DE UMA FORMA MAIS ELABORADA.

SEGUE ALGUNS MODELOS:

OBS: 

Fazer MANUALMENTE o mapa, e preferencialmente em folha sulfite (não esquecer de colocar nome, número e série).

OBRIGADA,

PROFª YASMIN

MATEMÁTICA - 3º SÉRIE

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 3º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 23/03 à 27/03. 


QUERIDOS ALUNOS,
COPIAR OS EXERCÍCIOS NO CADERNO (o Visto será dado no caderno, no retorno das aulas)


1) Calcule o coeficiente angular da reta que passa pelos pontos A(2, 3) e B(-3, 4).

2) Encontre a equação de uma reta com coeficiente angular m = 3/2, sabendo que ela passa pelo ponto A(5, 7).

3) Desenhe no plano cartesiano a reta que passa pelos pontos A(-2, 3) e B(3, 1) e calcule o seu coeficiente angular.

OBRIGADA,
PROFª YASMIN

Atividades de Sociologia - Profª Selma - 3ºs Anos

ATIVIDADE 1

- Pesquisar:

·         Os conceitos de Cidadania e Cidadão ontem e hoje.

·         Os Direitos e Deveres do Cidadão.

·         A Declaração Universal dos Direitos Humanos: artigos 1º,2º,3º, 6º,7º.

·         Democracia, Cidadania e Direitos Humanos no Brasil.

·         A Constituição Brasileira de 1988.

Os trabalhos deverão ser: manuscritos, resumidos, com conclusão própria, capa e bibliografia.

ATIVIDADE 2

- Responder as questões:

1) O que é cidadania plena e cidadania regulada?

2) É possível confirmar a existência de democracia e cidadania plena no Brasil? Justifique.

3) O que é uma Constituição? Explique a sua importância para um país.

4) Por que a Constituição brasileira é chamada de Constituição cidadã?

5) A Cidadania se refere a um conjunto de direitos e deveres ao qual um indivíduo está sujeito no ambiente social em que vive. Cite exemplos de direitos e deveres civis, políticos e sociais.

Atividades de Sociologia - Profª Selma - 2ºs Anos

ATIVIDADE 1

- Pesquisar:

·         A Diversidade Cultural e Regional da População Brasileira.

·         Imigrante, Emigrante e Migrante do ponto de vista sociológico.

·         Os conceitos de Aculturação e Assimilação.

·         Norbert Elias e os termos Outsiders e Estabelecidos.

Os trabalhos deverão ser: manuscritos, resumidos, com conclusão própria, capa e bibliografia.

ATIVIDADE 2

 - Responder as questões:

1) Explique a Diversidade da população brasileira. Cite três exemplos de povos que influenciaram essa diversidade.

2) Diferencie Imigrante, Emigrante e Migrante. Explique por que o imigrante não é simplesmente um turista.

3) O que é Aculturação? Cite 2 exemplos de povos no Brasil que tenham passado por esse processo.

4) Explique o processo de Assimilação. Cite três exemplos desse fenômeno no Brasil.

5) Qual é o aspecto mais importante da Assimilação no indivíduo?

6) Quem foi Norbert Elias e por que ele utilizou os termos outsiders e estabelecidos?

Atividades de Sociologia - Profª Selma - 1°s Anos

ATIVIDADE 1

- Pesquisar:

•                    O surgimento da Sociologia no contexto histórico das revoluções Industrial e Francesa.

•                    O que é a Sociologia, seu campo de atuação, e o trabalho do sociólogo.

•                    Senso Comum e Ciência. 

 Os trabalhos deverão ser: manuscritos, resumidos, com conclusão própria, capa e bibliografia.

 

ATIVIDADE 2

- Responder as questões:

1) Explique o surgimento da Sociologia no contexto histórico das revoluções Industrial e Francesa.

2) Quais os primeiros teóricos considerados os pais da Sociologia? Explique a importância de cada um.

3) Por que a Revolução Industrial trouxe modificações na maneira dos seres humanos se relacionarem? Quais os principais fatores dessas mudanças?

4) Explique por que a Revolução Francesa tornou-se o grande símbolo de mudança e um marco na história de Ocidente.

5) Diferencie o Senso Comum do Conhecimento Científico. Cite cinco características do Senso Comum e três características do Conhecimento Científico.

MATEMÁTICA 1º ano Ensino Médio

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 1º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 23/03 à 27/03. (Parte 2)


QUERIDOS ALUNOS,

• REALIZAR NO CADERNO AS ATIVIDADES A SEGUIR:

1) Considere os conjuntos A = {2, 4, 5, 12, 40, 53} e B = {9, 12, 30, 90}, determine:

a) A – B

b) A ∪ B 

c) A ∩ B

2) Sejam os conjuntos A = {1, 4, 5, 8}, B = {1, 2, 8} e C = {3, 8, 12}, determine:

a) A ∩ (B ∩ C)

b) A – (A ∩ B)

c) (A ∪ B) ∩ (B ∪ C)

3) Dados os conjuntos A = {2, 3, 4, 5, 6} e B = {-1, 0, 2, 3}, represente as operações abaixo.

a) A u B

b) A n B

c) A – B

d) B – A

4) Dados os conjuntos A = {números ímpares entre 1 e 10}, B = {múltiplos de 3 entre 1 e 12}, C = {números pares entre 3 e 11} e D = {múltiplos de 2 entre 1 e 9}, estabeleça as relações existentes entre os conjuntos através do Diagrama de Venn.

OBRIGADA,

PROFª YASMIN

MATEMÁTICA 1º ano Ensino Médio

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 1º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 23/03 à 27/03. 


QUERIDOS ALUNOS,

• PESQUISA:
• 

Folha separada para entregar (no retorno das aulas):

Fazer a tabela e colocar os seus respectivos significados (Fazer capa e não esquecer de colocar nome, número e série)

OBRIGADA

PROFª YASMIN 

Geografia 1º ano A e B Ensino Médio - Noite

Prezados alunos

Estamos atravessando um momento diferente, mas que certamente passará em breve! É muito importante esse isolamento neste momento para que possamos mais rapidamente voltar ao normal.
Portanto, por um período nossas atividades serão postadas aqui no blog. Faça aos poucos e monte uma pasta para que possamos no retorno, discutir os resultados.

Grande abraço!

Prof. Mauro Sergio


Atividades propostas:

1.) Pesquisa: Escolha um domínio morfoclimático brasileiro e descreva todas as suas características. Sugestões: Amazônia, Mares e Morros, Caatinga e Cerrado ou Araucárias e Pradarias.
2.) Mapa: Fazer o mapa da região escolhida, à saber: se for fazer a pesquisa sobre a Amazônia, faça o mapa da região Norte; Caso opte por Mares e Morros, Caatinga e Cerrado, pode fazer a região Nordeste, Sudeste ou Centro-Oeste. Finalmente, se optar por pesquisar Araucárias e Pradarias, faça o mapa da região Sul do Brasil.

Anexar ambas as atividades em um envelope ou pasta. Este será o seu portfólio para entrega ao professor!


Bom trabalho!

História 1º ano Ensino Médio - Noite

Prezados alunos

Estamos atravessando um momento diferente, mas que certamente passará em breve! É muito importante esse isolamento neste momento para que possamos mais rapidamente voltar ao normal.
Portanto, por um período nossas atividades serão postadas aqui no blog. Faça aos poucos e monte uma pasta para que possamos no retorno, discutir os resultados.

Grande abraço!

Prof. Mauro Sergio


Atividades propostas:

1.) Pesquisa: Escolha uma civilização antiga e pesquise sobre os diversos aspectos que envolvem essa civilização; algumas sugestões: mesopotâmicos, persas, egípcios etc. (Basta escolher um!)

2.) Mapa: Fazer o mapa da civilização escolhida (região onde se situava)

Anexar ambas as atividades em um envelope ou pasta. Este será o seu portfólio para entrega ao professor!


Bom trabalho!

MATEMÁTICA 3º ano Ensino Médio

Período de Quarentena (Covid 19)

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 3º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 16/03 à 20/03. (Parte 2)


QUERIDOS ALUNOS,

• COPIAR CONTEÚDO NO CADERNO (o Visto será dado no caderno, no retorno das aulas)

Equação geral

Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.

Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:

Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos , temos:

ax + by + c = 0

Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):

• se am + bn + c = 0, P é ponto da reta;
• se am + bn + c 0, P não é ponto da reta.

Acompanhe os exemplos:

• Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).

Considerando um ponto P(x, y) da reta, temos:

• Vamos verificar se os  pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo as coordenadas de P em x - y + 2 = 0, temos:

-3 - (-1) + 2 = 0 -3 + 1 + 2 = 0

Como a igualdade é verdadeira, então P  r.

Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:

1 - 2 + 2  0

Como a igualdade não é verdadeira, então Q r.

ASSISTIR A VÍDEO AULA :

https://www.youtube.com/watch?v=pRNnguDcR6Y

REALIZAR ATIVIDADES:

Caderno do aluno : Páginas 7 e 8

OBRIGADA,

PROFº YASMIN

MATEMÁTICA 3º ano Ensino Médio

Período de Quarentena (Covid 19)

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 3º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 16/03 à 20/03. 


QUERIDOS ALUNOS,

• COPIAR CONTEÚDO NO CADERNO (o Visto será dado no caderno, no retorno das aulas)

Distância entre pontos no plano cartesiano

No plano cartesiano conseguimos encontrar a distância através do par ordenado (x, y). Isso só é possível quando as pontos A e B estão alinhados horizontalmente ou verticalmente.

Quando os pontos estiverem em outra posição, como na diagonal, por exemplo, precisamos calcular a distância de outra forma.

Exemplo:

1) Encontre a distância entre A(2, 2) e B(3, 2):

A distância entre A e B é:

d(A, B) = B(3, 2) – A(2, 2) = 3 – 2 = 1

Fórmula para calcular a distância entre pontos

Para calcular a distância entre dois pontos temos a fórmula a seguir:

Essa fórmula serve para calcular a distância no plano cartesiano em que temos as coordenadas associadas a cada ponto. Por exemplo, A(x₁, y₁) e B(x₂, y₂).

Exemplo:

1) Calcule a distância entre A(2, 3) e B(3, 1).

Aplicando a fórmula, temos:

d(A, B) = √((2 – 3)² + (3 – 1)²) = √((-1)² + 1²) = √(1 + 1) = √2

Coeficiente Angular: Fórmula e Exemplos

O coeficiente angular é o valor que determina a inclinação de uma reta no plano cartesiano. Então, se o coeficiente for positivo a reta é ascendente, caso contrário, a reta é descendente.

No cálculo do coeficiente utilizamos a seguinte fórmula:

m = tg(θ)

Onde:

• m: é um número real qualquer;
• θ: é o ângulo que define a inclinação da reta.

Casos Particulares

• Quando θ = 0°: a tangente é nula;
• Quando 0° < θ < 90°: a tangente é positiva e está no 1º quadrante;
• Quando θ = 90°, ou seja, o ângulo é reto: não temos como calcular o coeficiente angular, pois não existe tangente para o angulo reto;
• Quando 90° < θ < 180°: a tangente é negativa e está no 2º quadrante.

Cálculo do Coeficiente Angular

O cálculo é feito a partir de dois pontos que correspondem a variação entre os eixos x e y.

A reta passa pelos pontos A(x_a, y_a) e B(x_b, y_b, assim:

Simplificando:

Onde:

• Δ_y: é a diferença entre os valores das ordenadas dos pontos A e B;
• Δ_x: é a diferença entre os valores das abcissas dos pontos A e B;

Exemplo:

Seja r uma reta qualquer, e A(-2, 3) e B(4, 1) pontos que a reta r passa. Calcule o coeficiente angular da reta r.

• m = Δy/Δx
• m = (y – y₀)/(x – x₀)
• m = (3 – 1)/(-2 – 4)
• m = 2/-6
• m = – ¹⁄₃

Como o coeficiente é negativo temos uma ideia de como é o gráfico, é descendente.

Equação da reta a partir do Coeficiente Angular e um ponto da reta

Seja a reta r com coeficiente angular m. Na reta r, consideremos os pontos P(x₀, y₀), tal que P ∈ r, e Q(x, y) um ponto qualquer da reta r de forma que r(Q ≠ P). Então:

Exemplo:

Seja uma reta r que passa pelos pontos P(2, 3) e o coeficiente m = 2, com x₀ = 2 e y₀ = 3. Determine a equação da reta r.

Resolução:

• y – y₀ = m(x – x₀) ⇒
• y – 3 = 2(x – 2) ⇒
• y – 3 = 2x – 4 ⇒
• 2x – y – 1 = 0
  
  
  ASSISTIR A VÍDEO AULA:https://www.youtube.com/watch?v=zolL2A1_bFk

OBRIGADA,

PROFESSORA YASMIN

MATEMÁTICA 1º ano Ensino Médio

Período de Quarentena (Covid 19)

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura           1º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 16/03 à 20/03. (Parte 2)


QUERIDOS ALUNOS,

• COPIAR CONTEÚDO NO CADERNO (o Visto será dado no caderno, no retorno das aulas)
• Subconjuntos

Dado um conjunto A, dizemos que B é um subconjunto de A, se B estiver contido em A, denotado por: B ⊂ A (B está contido em A). É o mesmo que dizer que B está dentro de A, ou seja, se todos os elementos de B estão dentro de A.

Exemplos:

Diagrama de Venn:  

Perceba que o conjunto B está literalmente dentro de A, portanto é subconjunto de A. Os elementos de B também são elementos de A.

C = {a, e, i, o, u} e D = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}

O conjunto das vogais C é subconjunto do conjunto do alfabeto da língua portuguesa D. Ou seja, o conjunto das vogais está contido no conjunto do alfabeto D.

Considerando que A e B são conjuntos, dizemos que A ⊂ B e B ⊂ A se, e somente se, A = B.

Exemplos:

Diagrama de Venn

Os elementos de A são os mesmo elementos de B.

A = {1, 2, 3} e B = {3, 2, 1}; a ordem dos elementos não importa, os dois conjuntos tem os mesmo elementos.

Observações:

• Todo conjunto é subconjunto de si mesmo, pois todos os seus elementos são elementos dele mesmo;
• O conjunto vazio é subconjunto de qualquer conjunto.

• Operações com conjuntos

União

Em muitos problemas em provas de vestibulares e do ENEM é necessário saber as operações com conjuntos. São elas: União, Interseção e Diferença.

A união de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A ou B.

• A ∪ B (Leia-se: A união B)

Definição de união

Sejam A e B conjuntos, a união de A com B é dada por:

• A ∪ B = {x ∈ U | x ∈ A ou x ∈ B}

• 

Propriedades

• A ∪ B = B ∪ A
• B ⊂ A ⇒ A ∪ B = A
• A ∪ ∅ = A
• (A ∪ B) ∪ C = A ∪ (B ∪ C) = A ∪ B ∪ C

Exemplos:

• {1, 2, 3} ∪ {4, 5} = {1, 2, 3, 4, 5}
• {a, b, c, c, c} ∪ {d} = {a, b, c, d}
• {1, 2} ∪ ∅ = {1, 2}

Interseção

A interseção de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A e B.

• A ∩ B (Leia-se: A interseção B)

Definição de interseção

Sejam A e B conjuntos, a interseção de A com B é dada por:

• A ∩ B = {x ∈ U | x ∈ A e x ∈ B}

Exemplos:

• {1, 2, 3, 4, 5} ∩ {5, 6, 7} = {5}
• {a, b, c} ∩ {b, c, d} = {b, c}
• {1, 2} ∩ ∅ = ∅

Propriedades

• A ∩ B = B ∩ A
• B ⊂ A ⇔ A ∩ B = B
• A ∩ ∅ = ∅
• (A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C
• (A ∩ B) ⊂ (A ∪ B)

Diferença

A diferença de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A mas não pertencem a B.

• A – B (Leia-se: a diferença entre A e B)
• 

Definição da diferença

Sejam A e B conjuntos, a diferença entre A e B é dada por:

• A − B = {x ∈ U | x ∈ A e x ∉ B}

Exemplos:

• A = {1, 2, 3, 4} e B = {1, 4, 6}
• B – A = {6}
• A – B = {2, 3}

Propriedades

• (A – B) ⊂ A
• A – ∅ = A
• ∅ – A = ∅
• A – (A ∩ B) = A – B

ASSISTIR A VÍDEO AULA :https://www.youtube.com/watch?v=XyO95CMs1SU&list=RDCMUCpb_oCNCS8PbUX6zHJ_fAsA&start_radio=1&t=70