MATEMÁTICA 3º ano Ensino Médio

Período de Quarentena (Covid 19)

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura          

 3º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 16/03 à 20/03. (Parte 2)


QUERIDOS ALUNOS,

• COPIAR CONTEÚDO NO CADERNO (o Visto será dado no caderno, no retorno das aulas)

Equação geral

Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.

Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:

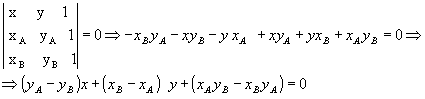
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos , temos:

ax + by + c = 0

Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):

• se am + bn + c = 0, P é ponto da reta;
• se am + bn + c 0, P não é ponto da reta.

Acompanhe os exemplos:

• Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).

Considerando um ponto P(x, y) da reta, temos:

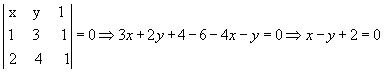
• Vamos verificar se os  pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo as coordenadas de P em x - y + 2 = 0, temos:

-3 - (-1) + 2 = 0 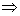-3 + 1 + 2 = 0

Como a igualdade é verdadeira, então P 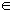 r.

Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:

1 - 2 + 2 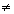 0

Como a igualdade não é verdadeira, então Q 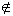r.

ASSISTIR A VÍDEO AULA :

https://www.youtube.com/watch?v=pRNnguDcR6Y

REALIZAR ATIVIDADES:

Caderno do aluno : Páginas 7 e 8

OBRIGADA,

PROFº YASMIN