MATEMÁTICA 1º ano Ensino Médio

Período de Quarentena (Covid 19)

E.E. Visconde de São Leopoldo
Disciplina: Matemática
Professora: Yasmin Moura           1º série A, B e C (Ensino Médio)

Atividades referentes à semana dos dias 16/03 à 20/03. (Parte 2)


QUERIDOS ALUNOS,

• COPIAR CONTEÚDO NO CADERNO (o Visto será dado no caderno, no retorno das aulas)
• Subconjuntos

Dado um conjunto A, dizemos que B é um subconjunto de A, se B estiver contido em A, denotado por: B ⊂ A (B está contido em A). É o mesmo que dizer que B está dentro de A, ou seja, se todos os elementos de B estão dentro de A.

Exemplos:

Diagrama de Venn:  

Perceba que o conjunto B está literalmente dentro de A, portanto é subconjunto de A. Os elementos de B também são elementos de A.

C = {a, e, i, o, u} e D = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}

O conjunto das vogais C é subconjunto do conjunto do alfabeto da língua portuguesa D. Ou seja, o conjunto das vogais está contido no conjunto do alfabeto D.

Considerando que A e B são conjuntos, dizemos que A ⊂ B e B ⊂ A se, e somente se, A = B.

Exemplos:

Diagrama de Venn

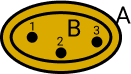
Os elementos de A são os mesmo elementos de B.

A = {1, 2, 3} e B = {3, 2, 1}; a ordem dos elementos não importa, os dois conjuntos tem os mesmo elementos.

Observações:

• Todo conjunto é subconjunto de si mesmo, pois todos os seus elementos são elementos dele mesmo;
• O conjunto vazio é subconjunto de qualquer conjunto.

• Operações com conjuntos

União

Em muitos problemas em provas de vestibulares e do ENEM é necessário saber as operações com conjuntos. São elas: União, Interseção e Diferença.

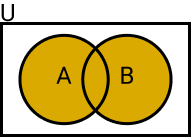
A união de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A ou B.

• A ∪ B (Leia-se: A união B)

Definição de união

Sejam A e B conjuntos, a união de A com B é dada por:

• A ∪ B = {x ∈ U | x ∈ A ou x ∈ B}

• 

Propriedades

• A ∪ B = B ∪ A
• B ⊂ A ⇒ A ∪ B = A
• A ∪ ∅ = A
• (A ∪ B) ∪ C = A ∪ (B ∪ C) = A ∪ B ∪ C

Exemplos:

• {1, 2, 3} ∪ {4, 5} = {1, 2, 3, 4, 5}
• {a, b, c, c, c} ∪ {d} = {a, b, c, d}
• {1, 2} ∪ ∅ = {1, 2}

Interseção

A interseção de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A e B.

• A ∩ B (Leia-se: A interseção B)

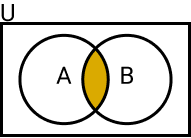
Definição de interseção

Sejam A e B conjuntos, a interseção de A com B é dada por:

• A ∩ B = {x ∈ U | x ∈ A e x ∈ B}

Exemplos:

• {1, 2, 3, 4, 5} ∩ {5, 6, 7} = {5}
• {a, b, c} ∩ {b, c, d} = {b, c}
• {1, 2} ∩ ∅ = ∅

Propriedades

• A ∩ B = B ∩ A
• B ⊂ A ⇔ A ∩ B = B
• A ∩ ∅ = ∅
• (A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C
• (A ∩ B) ⊂ (A ∪ B)

Diferença

A diferença de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A mas não pertencem a B.

• A – B (Leia-se: a diferença entre A e B)
• 

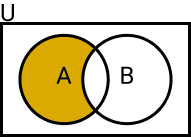
Definição da diferença

Sejam A e B conjuntos, a diferença entre A e B é dada por:

• A − B = {x ∈ U | x ∈ A e x ∉ B}

Exemplos:

• A = {1, 2, 3, 4} e B = {1, 4, 6}
• B – A = {6}
• A – B = {2, 3}

Propriedades

• (A – B) ⊂ A
• A – ∅ = A
• ∅ – A = ∅
• A – (A ∩ B) = A – B

ASSISTIR A VÍDEO AULA :https://www.youtube.com/watch?v=XyO95CMs1SU&list=RDCMUCpb_oCNCS8PbUX6zHJ_fAsA&start_radio=1&t=70